La guitare électrique
Théorie et pratique
Les cordes
La corde est, pour la guitare, qu’elle soit électrique ou acoustique, l’élément de base. Sans cordes, une guitare ne produit pas de son ; sans cordes, une guitare n’est pas une guitare. Une guitare électrique « normale » comporte 6 cordes de ce type ; il en existe également à 7, 8 et même 12 cordes, visant à enrichir le son de l’instrument. Chacune des cordes a une épaisseur différente. On nomme chacune des 6 cordes selon sa hauteur (sa note) lorsqu'on la joue à vide. L'accordage standard de des cordes est l'accordage EADGBE (qui est à lire Mi, La, Ré, Sol, Si, mi aigu).
Une corde de guitare électrique est, à la base, caractérisée par son épaisseur et sa composition (dans la plupart des cas, elle est en acier plaqué nickel : l'acier pour pouvoir être magnétisée suffisamment par le(s) micro(s) et le nickel pour être plus agréable au toucher). On se pose alors la question suivante :
De quels facteurs dépend la vibration de la corde ?
I. Fréquence et vibration
La fréquence d’une corde est exprimée en Hertz (Hz) et correspond à la déformation de la corde, sa vibration. Plus la fréquence est élevée, plus le son sera aigu. Plus la fréquence est faible, plus le son est grave.
Nous savons que lors de l’accordage d’une guitare, la rotation d’une cheville tend ou détend la corde correspondante, et augmente ou diminue alors sensiblement sa fréquence de vibration. C’est le principe même de l’accordage. De plus, lors de la pression d’une corde contre le manche, sa fréquence de vibration augmente également. Enfin, nous remarquons qu’une corde fine (comme la corde de Si) a une fréquence nettement plus élevée qu’une corde plus épaisse (par exemple la corde de La). Ainsi, nous pouvons alors supposer que la fréquence d’une corde dépend de sa tension, son épaisseur, et sa longueur vibrante.
Il existe une relation liant ces quatre grandeurs :
 | Avec : f la fréquence de la vibration en Herz Hz T la tension appliquée à la corde en Newton N µ la masse linéique de la corde en kg/m L la longueur vibrante de la corde en m. |
On pose v la vélocité de la corde, donnée par :
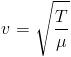 | Avec les même unités. |
D'où :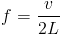 
On peut donc noter :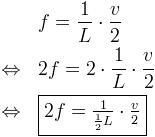
On peut déduire que lorsque la fréquence de la corde est multipliée par 2, la longueur est divisée par 2 ; et réciproquement.
Ainsi, on a :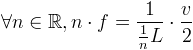 
La masse linéique et la longueur sont aisément calculables ou mesurables, mais comment déterminer la tension T ?
II. Fréquence et tension
On peut déterminer la tension exercée sur une corde de différentes manières :
... en accrochant un certain poids derrière une corde jusqu’à atteindre les mêmes résultats que pour la tension recherchée (fréquence, étirement, etc…)
... en mesurant l’allongement de la corde provoqué par la tension, ce qui amène à appliquer la loi de Hooke, énoncée en 1660 par le scientifique britannique Robert Hooke, par l’unique phrase en latin : « uc tensio sic vis » qui veut dire « telle extension, telle force », c’est-à-dire « l’allongement est proportionnel à la force ». Elle peut être exprimée de la façon suivante :
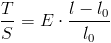 | Avec : T la force appliquée à la corde en N S la section de la corde en m2 E le module de Young en N/m2 l la longueur de la corde étirée en m l0 la longueur de la corde à vide en m |
Ainsi, connaissant la composition de la corde de guitare, et en mesurant la longueur de la corde à vide ainsi que sa longueur lorsqu'elle est étirée, nous pouvons calculer la force appliquée à la corde :
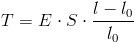avec les mêmes unités
NB : Le module de Young de l’acier est égal à 210000 MPa soit 210 * 109 Pa.
En la calculant à partir de la formule de base ; on obtient :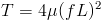
avec les unités du point fréquence et vibration.
III. Applications
Tous les résultats obtenus s’appliquent aux six cordes d’une guitare électrique. Ainsi, connaissant la fréquence, la longueur et donc la vélocité de chaque corde, on peut aisément tracer la courbe de la fréquence en fonction de la longueur vibrante de chaque corde de l’instrument ; la courbe du bas représentant la corde du Mi grave, la deuxième, celle du La, etc… :
Pour tracer ces courbes, nous nous basons sur la formule 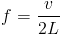, avec L=0.65m.
Chaque courbe correspondant à une des six cordes d'une guitare électrique accordée selon la GBTT, nous en connaissons la fréquence de vibration à vide, et pouvons en calculer la vélocité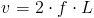 
.
Voici, pour chaque note, la vélocité de la corde :
| Note | Mi | La | Ré | Sol | Si | Mi |
| Fréquence à vide (Hz) | 82.41 | 110.0 | 146.8 | 196.0 | 246.9 | 329.6 |
| Vélocité (kg/Nm) | 107.1 | 143.0 | 190.8 | 254.8 | 321.0 | 428.5 |
NB : la droite rouge représente la limite du manche.
Sources
Voir la bibliographie.
La guitare électrique. Théorie et pratique. Projet de TPE.
LERAY Luc, LINDER Jean-Rodolphe, VAGINAY Yann