La guitare électrique
Théorie et pratique
Les frettes
Les frettes sont des pièces généralement métalliques qui délimitent deux cases : 
Lorsqu'on appuie sur une corde au niveau d'une case, la corde va toucher la frette, ce qui va réduire sa longueur vibrante et ainsi changer sa fréquence de vibration. La note engendrée sera donc différente.
Les frettes sont disposées d'une façon précise pour que la guitare sonne « juste ». Pour cela, elles sont disposées en fonction d'une gamme (suite de notes conjointes). On cherche donc à répondre à cette question : comment positionner correctement les frettes sur le manche d'une guitare électrique ?
La gamme conventionnelle de la guitare est la GBTT (Gamme Bien Tempérée Théorique).
Les démonstrations qui vont suivre ne sont donc valables que pour la GBTT.
I. Calcul des fréquences (par rapport à une fondamentale)
On appelle fondamentale la note de départ d'une gamme.
Différentes notes par rapport à une fondamentale (ici le La) :
| Nom | La (fondamentale) | La# | Si | ... | La (octave) |
| Rang / Degré | 0 | 1 | 2 | ... | 12 |
| Case sur la guitare | n | n+1 | n+2 | ... | n+12 |
NB : la GBTT de fondamentale la est composée des notes suivantes :
la ; la# ; si ; do ; do# ; ré ; ré# ; mi ; fa ; fa# ; sol ; sol# ; la (cette fois ci à l'octave)
L'intervalle entre deux de ces notes consécutives est appelé un demi-ton ; deux demi-tons correspondent à un ton.
On remarque que si# est la même note que do, de même pour mi# et fa.
Il faut aussi savoir que le bémol est l'«inverse» du dièse : ainsi, sib et la même note que la#.
I. A Fréquence d'une note à l'octave
Une note à l'octave à une fréquence double par rapport à la fondamentale : l'octave est l'intervalle entre une note de fréquence n et celle de fréquence 2n, est correspond donc à 12 demi-tons.
Soit f0 la fréquence de la fondamentale
Soit f1 la fréquence de la fondamentale à l'octave
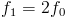
De même, si on considère que la fondamentale est de fréquence f1, alors la fréquence f2 de cette nouvelle fondamentale à l'octave est telle que :
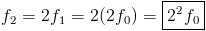
En général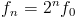 
avec n nombre d'octaves (donc n est un entier naturel).
NB : la suite des fréquence des notes aux octaves (0 octave = fréquence de la fondamentale, 1 octave, 2 octaves, etc...) est la suite géométrique de raison 2 et de terme initial la fréquence de la fondamentale.
I. B Fréquence d'une note de la gamme de rang n par rapport à la fondamentale
Soit une note de rang n et de fréquence fn
Sa note à l'octave sera de rang n+12 et de fréquence fn+12
On a donc :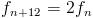 
Chaque note de la gamme peut être considéré comme une fondamentale, point de départ d'une nouvelle GBTT de cette note.
Soit n un rang quelconque,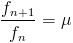 
reste constant.
En effet,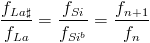 
(il s'agit là d'une propriété de la GBTT)
Donc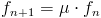 
, et par conséquent, on a :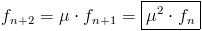 
En général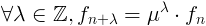 
De plus,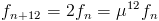 
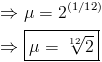
Soit une note de rang n et de fréquence fn
Soit f la fréquence de la fondamentale
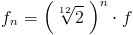
Donc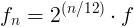 
avec n un entier relatif.
NB : la suite des fréquences des notes de la gamme est une suite géométrique de raison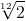 
et de terme initial la fréquence de la fondamentale.
II. Calcul de la disposition des frettes
Nous avons jusqu'à maintenant parlé des relations qu'il existe entre une fondamentale et des notes d'une même gamme (la GBTT).
Il nous reste à déterminer la position des frettes (les frettes séparent le manche en demi-tons) : quelle distance sépare la nième frette du sillet ?
II. A Rappel
Si on veut que la fréquence d'une corde soit multipliée par n, il faut diviser la longueur vibrante par n (ceci a été démontré dans la partie cordes).
Soit f la fréquence d'une corde de longueur L
Soit f' la fréquence d'une corde de longueur L'
Soit k un réel
On a : 
II. B Longueur vibrante de la corde correspondant à une note
Soit fn la fréquence d'une note de rang n, par rapport à la fondamentale (on prend ici comme fondamentale la note que donne la corde à vide de longueur L, de fréquence f)
Soit Ln la longueur du segment de la corde qui engendre la note de rang n. Autrement dit, Ln est la distance entre le chevalet et la frette n.
On a :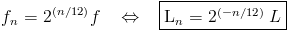 
avec n un entier naturel.
II. C Rapport des distances entre le chevalet et deux frettes consécutives
En reprenant la formule précédente et avec L la longueur de la corde (distance entre le sillet et le chevalet) et L1 et L2 les distances entre le chevalet et respectivement la 1ere et la 2e frette, on a :
Ainsi Le rapport des distances entre le chevalet et deux frettes consécutives est de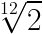 
II. D La position des frettes
Soit Pn la position de la frette n (distance entre le sillet et la frette n) :
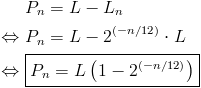
avec n un entier naturel.
L, Ln, et Pn sont tels que sur le schéma :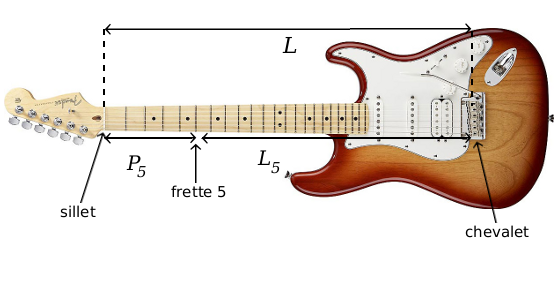
Résumé
| Rang | 0 (fondamentale) | 1 | 2 | n | 12 (octave) |
| Fréquence | f | 21/12f | 21/6f | 2n/12f | 2f |
| Longueur vibrante de la corde | L | 2(-1/12)L | 2(-1/6)L | 2(-n/12)L | L/2 |
| Position de la frette | 0 | L(1-2(-1/12)) | L(1-2(-1/6)) | L(1-2(-n/12)) | L/2 |
Sources
Voir la bibliographie.
La guitare électrique. Théorie et pratique. Projet de TPE.
LERAY Luc, LINDER Jean-Rodolphe, VAGINAY Yann